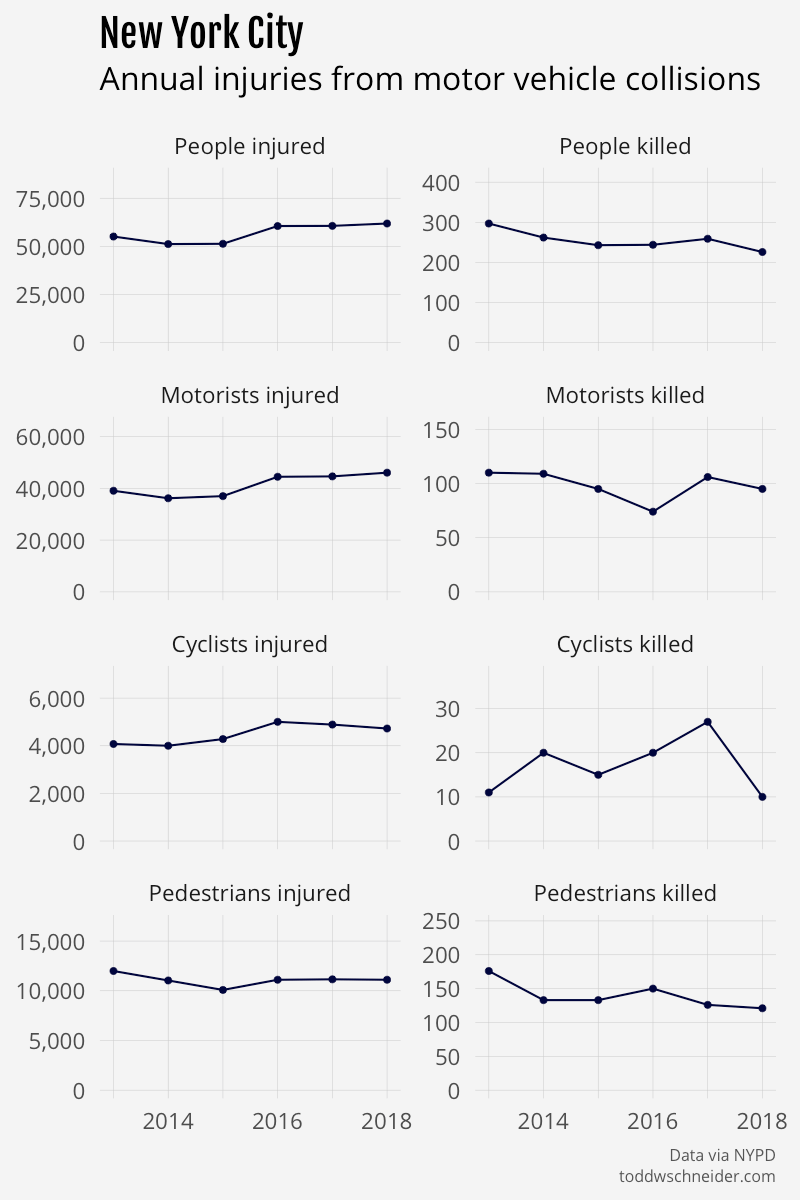
The City of Chicago now publishes trip-level data for every ride-hail trip taken since November 1, 2018. Chicago isn’t the first major US city to make ride-hailing trip data publicly available—New York has published Uber and Lyft data since 2014—but the Chicago dataset includes additional fields, most notably fare amounts, that provide new insights into the ride-hailing landscape.
In particular, although the dataset does not explicitly indicate when high-demand “surge” pricing was in effect, I used the available fields to reverse engineer the historical surge pricing map based on a robust regression model. More to come about the methodology, along with challenges and caveats. All code used in this post is available on GitHub. As I write this in March 2020, the dataset includes 129 million trips from November 1, 2018 through December 31, 2019. It is scheduled to update quarterly in the future.
You can play around with the map below to see estimated surge pricing multipliers by time and neighborhood. I’ve highlighted some notable events with elevated pickup activity and/or surge pricing, for example at the conclusion of The Rolling Stones concert at Soldier Field on June 25, 2019, when fares were 3x more expensive than usual.
Click here to view map in full screen or on a mobile device
In addition to estimated surge multipliers, the map shows modified z-scores, which represent pickup activity in an area compared to the median for that time of day and day of week. Positive z-scores mean more pickups than normal. For example, the area near Soldier Field saw 154 pickups at midnight after the Stones concert, while a median Wednesday midnight sees 9 pickups with a median absolute deviation of 2.5. Those numbers produce a large modified z-score of 39, meaning way more pickups than normal. (The “modified” part in modified z-score refers to the use of the median and median absolute deviation instead of the mean and standard deviation, which reduces the impact of outliers.)
It’s often interesting to compare the map of surge multipliers to the map of modified z-scores, since Uber and Lyft both state that surge pricing goes into effect when there are more riders than drivers in an area. The dataset does not explicitly tell us how many drivers are available at any given moment, but it seems like a reasonable assumption that sudden demand spikes and higher-than-normal pickup activity would often coincide with rider demand outstripping driver supply.
Anatomy of a major surge pricing event: The Rolling Stones No Filter Tour
The conclusion of the aforementioned Rolling Stones No Filter Tour show on June 25, 2019 appears to have been one of the most severe surge pricing events in the dataset. I isolated trips that began near Soldier Field on the Near South Side, then compared surge prices to pickup counts at each 15-minute interval. The graph shows that surge prices and pickup activity both started to increase around 11:30 PM. Peak surge occurred between midnight and 12:30 AM, which coincided with the largest number of pickups.

I couldn’t find the exact time they played each song on the setlist, but I’d guess that the encore of “Gimme Shelter” and “(I Can’t Get No) Satisfaction” began just before midnight, and the 11:30 PM pickups peak represents people who tried to beat the traffic and skipped the encore, while the larger 12:15 AM pickups peak includes the folks who stuck around until the very end. The 11:30 PM departures paid a significantly lower average surge of 1.7x compared to 3.2x for the 12:15 AM crowd, though with ticket prices already averaging $500, I’m not so sure that would have been a major consideration.
The June 25 show was the Stones’s second Soldier Field date; they kicked off their 2019 North American tour a few nights earlier on June 21, and the ride-hailing activity patterns look pretty much the same. The first show saw a bit more pickup activity than the second show, but a slightly lower peak surge rate of 2.9x.
The next-most severe Soldier Field surge pricing events belonged to another major concert tour, though one that perhaps catered to a different audience than the Stones. K-pop supergroup BTS played two Soldier Field dates on May 11 and 12, 2019 as part of their Love Yourself: Speak Yourself world tour. The average post-concert surge prices on night one and night two reached as high as 2.5x.
Bears games show less evidence of post-game surge pricing, but there’s a big caveat
Soldier Field is home for the NFL’s Chicago Bears, but strangely enough, Bears games do not show much evidence of surge pricing compared to The Rolling Stones and BTS concerts, even though Bears games do exhibit similar demand spikes at the conclusion of games.
Here’s a representative graph of ride-hail activity immediately following a Bears home game. (Apologies to Bears fans, but as an Eagles fan, I must confess that I look back fondly on the Double Doink.)

None of the Bears home games in the dataset appear to have produced major spikes in surge pricing. The biggest post-game pickup spikes were a pair of 2019 regular season Thursday night games against the Packers and Cowboys, both of which show similar patterns to the Eagles game: a large spike in post-game pickups, but only a small corresponding increase in surge prices. The biggest post-game surge I could find occurred after a December 2019 Sunday night game against the Chiefs, but the peak surge of 1.4x was still significantly lower than the rates seen at the Stones and BTS concerts.
One possibility is that drivers are somehow more “aware” of Bears games than concerts, so they’re more likely to make themselves available in the vicinity of Soldier Field after Bears games than concerts, and the excess supply of cars prevents surge pricing from kicking in. The dataset does not provide any information on how many drivers were available in an area at a given time, so this would be a difficult idea to test, but there might be a creative way to get at it. We also don’t know how many people tried to hail a ride but then for whatever reason didn’t. For example, though pickups peaked at around 300 per 15 minutes after both the Stones concert and the Eagles game, maybe there were more people trying to hail rides after the concert.
There are plenty of theories we could come up with to explain the Bears/Stones discrepancy, but if I had to guess, the most likely explanation is a major caveat that runs throughout this entire post: it seems like most of the major surge events citywide occurred in Q2 2019—specifically between March 29 and June 30—so much so that it makes me wonder if there is an error or other hidden bias in the dataset. If there is a Q2 2019 bias, then regardless of whether it’s a data error, a change in surge pricing algorithms, or something else, the May/June concerts might have more severe surge pricing than the September–January Bears games due to a hidden variable, not an underlying truth that concerts produce higher surge prices than football games.
The United Center tells a similar story. Located on the Near West Side, it hosts the NBA’s Bulls and NHL’s Blackhawks, a number of major concerts from Ariana Grande to Travis Scott, and other one-off events like UFC 238 and a Michelle Obama book reading. Much like at Soldier Field, the highest surge pricing rates seem to come at the conclusion of concerts, but again I’m concerned about the Q2 2019 bias.
Neither the Bulls nor the Blackhawks made their respective leagues’ playoffs in 2019, so there weren’t many NBA/NHL games that took place in April/May/June. The few games that took place in April 2019 did show some significant surge pricing compared to games that took place in other months. For example, the Bulls hosted the Knicks on both April 9, 2019, and November 12, 2019. Both games were on Tuesday nights, both saw similar numbers of post-game pickups, yet only the April 9 game had significant surge pricing.
The two biggest United Center concerts, as measured by spikes in total pickups, belonged to Mumford & Sons on March 29, 2019, and Travis Scott on December 6, 2018. Both concerts had similar-sized spikes in pickups, but post-Mumford & Sons surge pricing reached 2.7x, while post-Travis Scott peaked at a more mild 1.4x. Again though, March 29 was the beginning of the 3-month period of elevated surge pricing citywide, so it’s possible that some hidden bias accounts for the elevated surge.
Of course I’ve cherry-picked these examples to fit a narrative, but you can head over to GitHub to see surge pricing graphs for every date on the United Center events calendar.
Geographically widespread surge pricing events
Concerts and sporting events are obvious candidates for surge pricing because they involve large groups of people trying to leave the same place at the same time, which could easily overwhelm the supply of available drivers. But there are also examples of more geographically diffuse surge pricing events, often coinciding with holidays or inclement weather.
One of the biggest citywide surge incidents occurred on the morning of Monday, April 29, 2019. It rained heavily that morning, and by 6:00 AM, surge prices reached 2x across most of the city’s North Side. As rush hour peaked around 8:00 AM, riders stretching from Lake View to Hyde Park were paying 2-3 times their normal fares. By 9:30 AM, the surge had died down and fares were back to normal.
If you look at the map of z-scores during the April 29 surge, demand was somewhat elevated compared to a typical Monday morning, but not dramatically so, and certainly not as severely as after a big concert. Again, we don’t know exactly how many drivers were available that morning. It’s possible that the bad weather initially made drivers less inclined to work, which led to high surge prices to incentivize more drivers to become available.
Other events that caused elevated demand across the entire city include New Year’s Eve, Super Bowl LIII, Saint Patrick’s Day Parade, Pride Parade, and the late night hours of Thanksgiving Eve—the unfortunately-titled “Blackout Wednesday.” Of that list, the 2019 Pride Parade looks to have generated the highest surge pricing, but again it occurred during the Q2 2019 era of generally elevated surge pricing, so it could be an artifact of that as opposed to something more meaningful.
Surge pricing seasonality by location and time of week
The unexplained Q2 2019 discrepancy makes it difficult to say anything meaningful about general surge pricing trends, but it seems like there are some patterns when you look at certain regions by time of week. For example, on the North Side—a generally affluent area with high rider demand on weekday mornings as people commute into Central Chicago—weekday surge prices tend to be highest in the morning. The magnitude is more severe during the Q2 2019 period, but the 8:00 AM–9:00 AM hour appears to be the most expensive throughout the year.
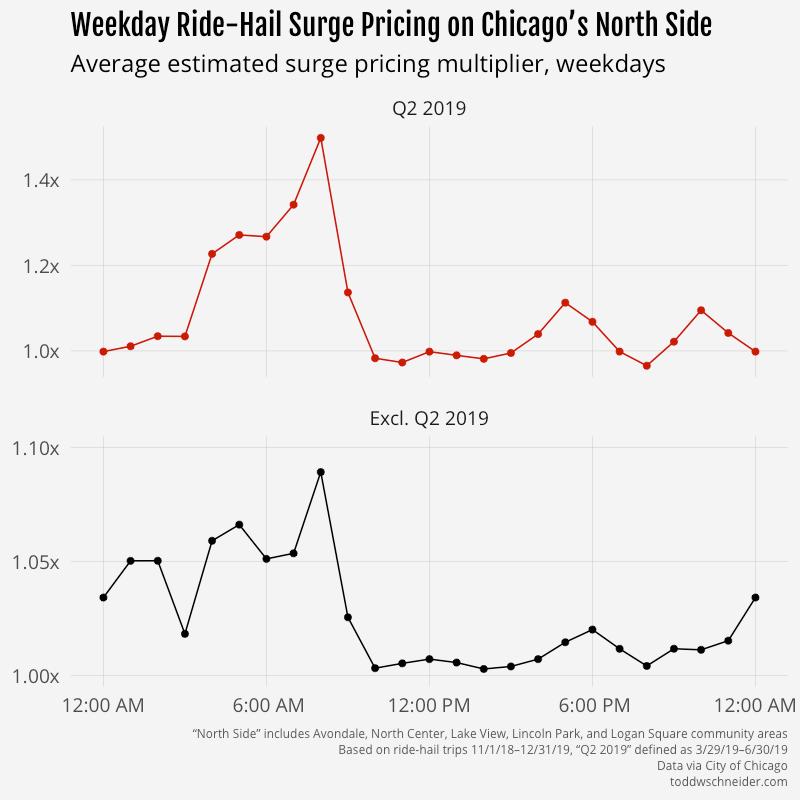
The North Side also sees a lot of pickups on weekday afternoons, but surge prices are significantly lower during afternoons compared to mornings. One possibility is that there are more cars available in the afternoon. The weekday afternoon route from Central Chicago to the North Side is very common, so maybe that produces a surplus of available drivers on the North Side, which in turn drives down fares for afternoon riders getting picked up on the North Side. I didn’t dig into that idea any deeper, but it could make for an interesting follow up.
In Central Chicago, where demand is highest on weekday afternoons as people head home after work, surge prices are highest during afternoon rush hour.
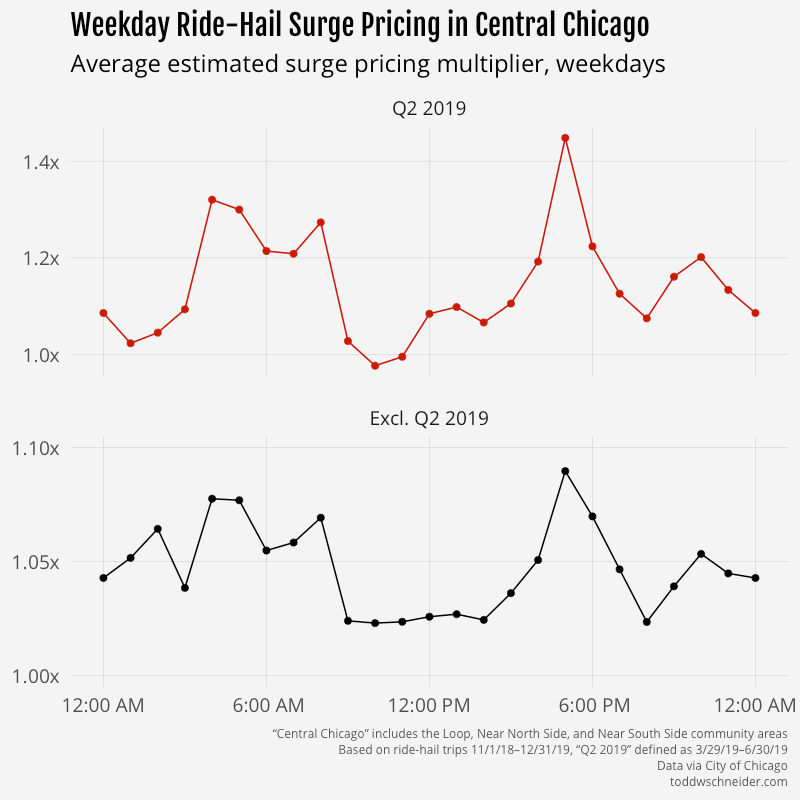
And on the West Side, where demand is generally highest on weekend evenings, surge prices are highest in the late night weekend hours.

Robust regression methodology to estimate historical surge prices
The dataset does not explicitly tell us when surge pricing was in effect, but it provides fields that allow us to estimate: trip distance, travel time, and fare amount. Uber and Lyft do not say exactly how they determine fares, but they both indicate on their websites [Uber, Lyft] that fares are based on a combination of distance and time.
I first calibrated a robust regression model of fare as a linear combination of distance and time, then estimated the surge multiplier for each trip as its actual fare divided by the baseline predicted fare. For example, if a 4-mile, 15-minute trip had an actual fare of $15, but the baseline model predicted it should have been a $10 fare, then the estimated surge multiplier for that trip is 1.5x.
After I estimated multipliers for each trip, I bucketed by pickup census tract and timestamp rounded to 15 minutes, and took the simple unweighted average of all surge multipliers within each bucket. In some cases, when tract-level info wasn’t available, I aggregated by the larger community area geographies.
The naive temptation for the baseline model might be to fit a linear regression via ordinary least squares, for example using R’s lm() function. However, in this case I don’t think that’s the right way to fit the baseline model, because an OLS linear regression will find parameters that make the average predicted fare equal to the average actual fare. But we don’t want to fit our baseline model against all fares, rather we want to fit it against some notion of “typical” fares, excluding surge and other pricing abnormalities like discounts. This presents a circular logic problem:
- We want to establish a baseline fare model so that we can figure out which fares differ from the baseline
- We want to exclude abnormal fares when determining the baseline model
- We don’t know which fares are abnormal until we’ve established the baseline model
Robust regression methods are designed to address this circular problem. I chose the rlm() function from R’s MASS package with the “MM” option, which uses an iterative process to find coefficients of a linear model, determine outliers based on those coefficients, downweight or even remove the outliers entirely, find new coefficients, and repeat until some convergence criteria are met.
I found that the coefficients from the robust model implied base fares were 12% lower than implied by the OLS model during the Q2 2019 period, and 3% lower in other periods. The robust coefficients also aligned more closely with the indicative rate cards posted on Uber and Lyft’s websites, which provides some reassurance that the robust methodology is a reasonable estimate of non-surge fares.
Why were surge prices so high in Q2 2019?
The period from March 29, 2019 through June 30, 2019 appears to contain a disproportionate number of major surge pricing events compared to the rest of the dataset.

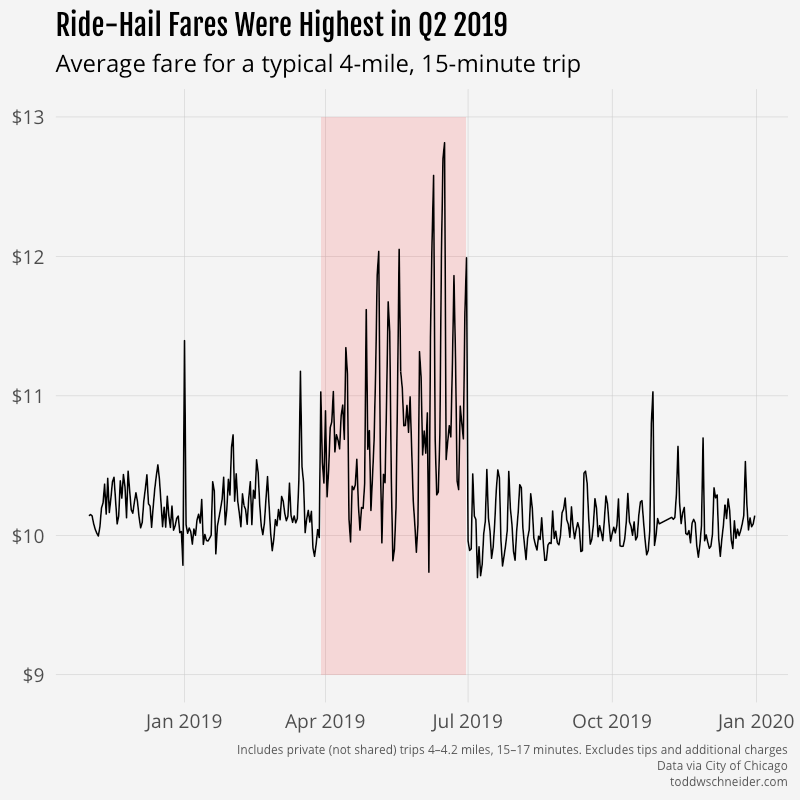
My first thought was that maybe Uber and/or Lyft changed their base fare rates during that time period, so I split the dataset into three pricing regimes—before, during, and after Q2—and calibrated separate robust regression models for each regime. Here are the resulting model coefficients:
| Time period | Intercept | Fare per mile | Fare per minute |
|---|---|---|---|
| Before 3/29/19 | $1.81 | $0.82 | $0.28 |
| 3/19/19–6/30/19 | $2.13 | $0.82 | $0.27 |
| After 6/30/19 | $1.87 | $0.82 | $0.27 |
The coefficients on distance and time were nearly identical in all 3 regimes: 82 cents per mile, plus 27–28 cents per minute. The intercept for the Q2 regime was around 30 cents higher than for the other periods, which amounts to a bit over 2% of the average $13 fare.
The fact that the robust regression coefficients from Q2 are not drastically different than the periods before and after argues, but does not prove, that base fare rates were not different during the Q2 period. My best guess is that one or both of Uber and Lyft made some changes that resulted in more aggressive surge pricing in Q2 2019, but then reverted those changes on or around July 1. I’m still wary though that there could be a data reporting error; it will be interesting to see what happens as more trip data is published in the future.
There are other possibilities to consider, e.g. maybe there’s a spring seasonal effect, perhaps due to elevated rider demand following the long, cold winter. Unfortunately it’s hard to know much about time-of-year seasonality since there’s only one year of data available. The particularly abrupt apparent surge pricing decrease on July 1 argues against a seasonal effect, and to me suggests something like an algorithm change or a data reporting error.
There was a story from May 2019 about drivers in Washington, D.C. attempting to manipulate surge pricing algorithms by simultaneously turning off their apps to create the appearance of a driver shortage. I have no particular insight into the strategy’s existence, effectiveness, or presence in Chicago, but I suppose it’s possible that the story led to Uber and Lyft changing their surge pricing algorithms.
I’m not sure how we could confirm an algorithm change, as Uber and Lyft don’t seem likely to reveal their secret sauce anytime soon. For what it’s worth, March 29, 2019—the first day of elevated surge estimates—was also Lyft’s first day as a publicly-traded company. Uber’s IPO followed a few weeks later on May 10. I suppose it’s as least possible that they increased their surge rates around then in an effort to demonstrate revenue growth to Wall Street, but it strikes me as unlikely given all of the coordination required.
Additional caveats and challenges
Surge pricing is one of many factors beyond time and distance that can impact a single trip’s fare. The dataset does not provide explicit info about these additional factors, so I made some oversimplifications and assumptions and that are worth noting.
Uber and Lyft both offer an array of vehicle classes—standard, luxury, SUV, etc.—each of which has a different base rate. The dataset does not include the vehicle class for each trip, so the model assumes that all fares have the same base rate, which we know isn’t true. The robust regression model will tend to fit the baseline against the most “typical” fares, which might include only the standard vehicle tier. If that’s the case, and, say, trips from the central business district are more likely to request luxury vehicles, then it could appear that the CBD has higher “surge prices”, when in reality the higher prices are driven at least in part by corporate riders’ tendency to request more luxurious vehicles.
Surge pricing makes fares more expensive than normal, but Uber and Lyft sometimes offer promotional discounts that make fares cheaper than normal. I’m hopeful that the robust regression methodology handles discounts roughly correctly by identifying them as outliers and downweighting them, but there’s no easy way to confirm. There have been some reports that both companies are trying to cut back on discounts, which could make it appear that surge pricing is increasing over time, even though the underlying reality is a decrease in discounts as opposed to an increase in surge pricing.
Uber and Lyft both provide upfront prices based on expected time and distance, which in turn are presumably based on routing algorithms that take into account factors like traffic and weather. If a trip’s actual time and distance end up differing from the expectations baked into the upfront price, my methodology might incorrectly interpret the fare as either a surge or a discount. Both companies say that they revise upfront fares for trips that materially deviate from expectation, so hopefully that mitigates some of this concern.
We could try to control for some of these hidden factors in the baseline model, for example by adding explanatory variables based on geography and time of week, but without any actual data that isolates the effects of surge pricing, discounts, vehicle class, and upfront pricing, I’d worry that the results would end up as a mishmash of all of them, which is essentially what the existing baseline model already is.
The City of Chicago takes some measures to protect rider, driver, and company privacy in the data. I very much support the privacy measures overall, but they do make it somewhat harder to estimate surge pricing. In particular, the dataset has the following privacy-oriented limitations:
Fares are rounded to the nearest multiple of $2.50. This reduces the precision on surge multiplier estimates, especially for smaller fares. For example, if a trip’s baseline expected fare is $4.00, but a surge of 1.5x is in effect so the actual fare is $6.00, that surge will never show up in the data because both $4.00 and $6.00 will round to $5.00. I attempted to control for this by excluding shorter trips when calculating average surge multipliers. Specifically, I restricted to fares that were at least 1.5 miles or 8 minutes. One nice reassurance is that my baseline model coefficients happen to align closely with the standard vehicle rates posted on Uber and Lyft’s websites.
Pickup and drop off timestamps are rounded to 15-minute intervals. If we’re looking at trips in an area between 12:00:00 PM and 12:14:59 PM, we won’t know which ones were at 12:00, 12:01, 12:02, etc. If surge pricing went into effect for just 2 minutes, the surge trips would get averaged in with trips from the other 13 minutes of the interval, resulting in a smoothed-out average surge multiplier. Additionally, the timestamps refer only to the time of pickup, but it might be relevant to know the timestamp when each rider submitted their ride request, as I’d imagine that’s a trigger for surge pricing algorithms.
Pickup and drop off geographies are imprecise, and sometimes redacted. Surge pricing can go into effect in very localized regions, as small as a few city blocks. But the Chicago dataset only provides pickup and drop off locations by census tract. Census tracts vary in size, but are almost always larger than a few city blocks, so if a surge goes into effect for a subregion of a tract, the tract-level aggregate will be smoothed-out. Additionally, census tracts are deliberately dropped in some cases where there are not enough pickups or drop offs over a 15-minute window. In such cases, locations are aggregated up to the community area level, which further reduces the precision of surge pricing estimates. Census tract-level data is available for about 75% of the trips in the dataset, the other 25% use community areas.
There are more general caveats beyond the potential hidden factors and privacy measures described above. Some trip records contain obvious junk data, e.g. a $1,000 fare for a 3-minute, 1-mile trip. I applied some heuristics to remove rows where I thought the data was an error, see GitHub for the exact logic.
The dataset does not provide info on which ride-hail company provided each trip, so there’s no obvious way to tell if Uber and Lyft have significantly different surge pricing behavior. As of March 2020 there are three companies registered to do business in Chicago: Uber, Lyft, and Via. A third party estimates their market shares as of November 2019 as 72% Uber, 27% Lyft, and 1% Via, which is not too far off from the known market shares in New York. (Of note, the New York dataset does include the company associated with each trip, but NYC does not provide fare info, so there’s no way to estimate surge pricing in NYC.)
In addition to the fare amount for each trip, the dataset also includes tips and “additional charges”, which cover taxes, fees, and tolls. I made the assumption that surge multipliers affect only the fare component, which seems consistent with the data, though I doubt the results would change much if I had used [fare + additional charges] as the dependent variable instead of fare only. Chicago added a new ride-hail tax in early 2020, which is not yet reflected in the data, but it will be interesting to see what happens as the dataset grows.
A note on shared rides
Shared rides present another challenge, because it’s not as clear how to establish a baseline fare. A more inconvenient route for a shared trip will increase both the time and distance, but it might make the fare cheaper since the rider might need an incentive to accept the longer route. About a third of shared trip requests don’t get matched, which is another important factor in determining the fare. I calibrated robust regressions for share-requested fares using time, distance, and whether the trip was matched, but it might make more sense to use “expected time/distance if following the most direct route” instead of actuals. I would want to do more research and investigation before feeling more confident about shared trip pricing. Making matters more confusing, it seems like there was a change in the way shared trip distances are reported starting in November 2019, when the average shared trip distance increased dramatically.
For the purposes of this post, I excluded trips with share requests when estimating surge multipliers, but I included trips with share requests when measuring rider demand, e.g. modified z-scores and pickup counts in the various graphs.
About 20% of trips in the dataset include a share request. Of those, about 68% get pooled into a shared trip, with the other 32% going unmatched. It seems like shared trips have become less popular over time; the months toward the beginning of the dataset have a higher percentage of share requests (~27%) and a higher match rate (~72%), but as of Q4 2019, only 15% of trips include a share request, with 60% of share requests get matched. See the shared trips section of the ride-hailing dashboard for the latest data.
Future work, and what about a surge pricing model?
There’s a lot of interesting work that could be done comparing Chicago’s public taxi and ride-hail datasets. As of December 2019, baseline private ride-hail trips are cheaper than taxis, and it looks like the “breakeven” surge is around 1.2x, meaning thax ride-hail trips are cheaper than taxis as long as the surge rate is 1.2x or lower. If you take tips into account, the breakeven is closer to 1.4x, since 95% of taxi trips but only 22% of private ride-hail trips include a tip. The city instituted a new ride-hail tax in January 2020, which will presumably lower the breakeven, and it will be interesting to see if rider preferences shift at all in favor of taxis.
I experimented a bit with some regression models to predict surge pricing as a combination of modified z-scores, sudden demand spikes, and other variables. The resulting models didn’t fit the data particularly well, and they didn’t feel “useful”, because many of the independent variables wouldn’t be known by anybody in real time. There might be some clever additional variables to include, in particular maybe there’s a way to estimate the supply of drivers over time. An agent-based approach that takes into account rider, driver, and company incentives strikes me as potentially the most satisfying option, but would also be much harder to formulate and calibrate.
Appendix: robust regression simulation and intuition
As something of a sanity check on the robust regression methodology, I simulated 1,000 trips with the following assumptions:
- Trip distance distributed uniformly between 1 and 10 miles
- Average speed distributed uniformly between 10 and 30 miles per hour, which implies a travel time in minutes
- Base fare = $1.87 + $0.82 * miles + $0.27 * minutes
- 20% chance of surge pricing. If surge pricing applies, the multiplier is distributed uniformly between 1.1 and 3
- 20% chance of a discount. If discount applies, it is uniform between 10% and 20%, subject to a max of $6
- Actual fare = [Base fare] * [Surge multiplier] - [Discount]
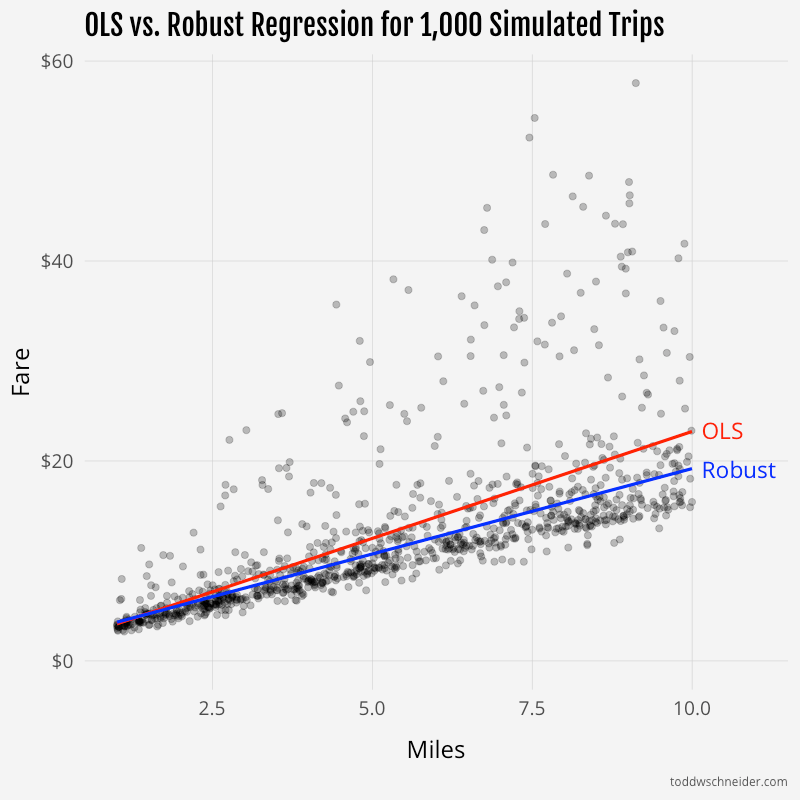
I then fit linear models of actual fare as a function of distance and time via ordinary least squares and robust methods. The robust model “recovered” the exact base fare parameters of $1.87, $0.82, and $0.27, while the OLS model fit parameters of $1.56, $1.00, and $0.35.
For the average simulated trip of 5.5 miles and 16.5 minutes, the OLS model predicts a fare of $12.79, 18% higher than the $10.84 fare predicted by the robust model. In some circumstances, the OLS model might be more useful. For example, if all you knew was that you were about to take a 5.5-mile, 16.5-minute trip in this simulated world, the OLS model represents the expected value of what you’re going to pay. But if you’re trying to decompose your payment into a base fare, surge multiplier, and discount, then the robust model is closer to the underlying truth. (Of course in this case we know the underlying truth because we created it; in real life we don’t have that luxury.)
You can see from the trendlines that the OLS model is “pulled” up by the outlier surge prices:
If you want to generate similar simulated data on your own, here’s some R code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | |
And again, all code used in this post is available on GitHub.